
Oliver Byrne's edition of Euclid
An unusual and attractive edition of Euclid was published in 1847 in England, edited by an otherwise unknown mathematician named Oliver Byrne. It covers the first 6 books of Euclid's Elements of Geometry, which range through most of elementary plane geometry and the theory of proportions. What distinguishes Byrne's edition is that he attempts to present Euclid's proofs in terms of pictures, using as little text - and in particular as few labels - as possible. What makes the book especially striking is his use of colour. Incidentally, at the time of its publication the first 6 books, which are the ones concerrned with plane geometry, made up the basic mathematics curriculum for many students.
With the financial support of several undergraduate organizations at UBC - the Alma Mater Society of UBC, the Science Undergraduate Society at UBC, and the Undergraduate Mathematics Club - and the cooperation of the Special Collection Division of the UBC Library, we have had the entire edition photographed by Greg Morton at UBC Biomedical Communications We hope to mount eventually on this site digital images of all of the photographs. We imagine that it will serve as an interesting resource for geometry projects all over the world.
We have mounted all of Byrne's book, but in the organization of the site is by no means final. We are still experimenting with the images to improve their quality, and sooner or later the structure found for Book VI, which is much better than the rest, will be transported to the other books. If you have any suggestions we'll be pleased to hear from you.
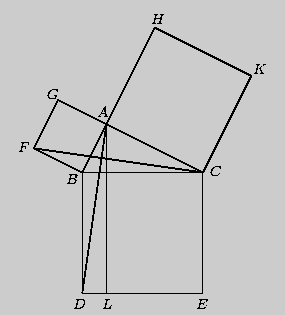
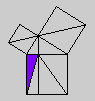
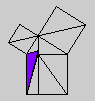
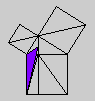
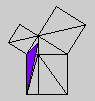
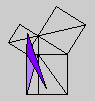
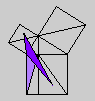
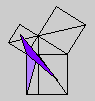
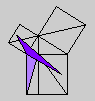
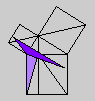
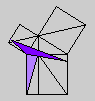
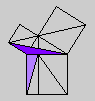
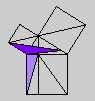
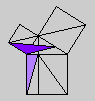
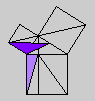
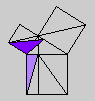
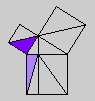
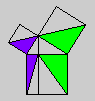
Whether or not Byrne's efforts complicate or simplify Euclid is an interesting and debatable point. Parts of Byrne's attempt to design `colour-coded' mathematical proofs are more successful than others, but it is our hope that even the less successful parts can serve as themes for discussion if not models for imitation. The title page of Byrne's edition, at any rate, illustrates the basic concept of the book rather nicely with a single figure illustrating Euclid's Proposition 47 (Pythagoras' Theorem).
The copy from which this image was taken is in the Colbeck collection of the Library of the University of British Columbia. It was purchased in auction in 1974 for about $300. Byrne's edition became well known recently when extracts from it were included and discussed in the second of Edward Tufte's books on graphical design. A copy of Byrne's book was auctioned in November, 1996 for US $3220.
Byrne is also the author of a book Dual arithmetic also reviewed in A Budget of Paradoxes. The proposal is to replace the usual decimal notation ...
De Morgan's editor, the American historian of mathematics David Eugene Smith, doesn't like the idea of Byrne's edition of Euclid, either, but unfortunately we do not have De Morgan's opinion of it.

We have mounted all of Byrne's book, but in the organization of the site is by no means final. We are still experimenting with the images to improve their quality, and sooner or later the structure found for Book VI, which is much better than the rest, will be transported to the other books. If you have any suggestions we'll be pleased to hear from you.
The collection
- Introduction
- Euclid's Book I
- Euclid's Book II
- Euclid's Book III
- Euclid's Book IV
- Euclid's Book V
- Euclid's Book VI
More about the edition
Oliver Byrne's edition of Euclid was published in 1847 by William Pickering and printed by Chiswick Press. This press has been called by Ruari McLean, a well known author of books on printing and typography, the foremost name in Victorian book design and synonymous with good typography and printing throughout the [Victorian] period. Chiswick Press was operated at that time by Charles Whittingham, nephew of its founder, and Pickering and Whittingham collaborated in a number of innovative publications around that time. Pickering was particularly known for elegant title pages. The initial letters for this edition were made by Mary Byfield, who worked regularly at wood-engraving for the firm.McLean calls Byrne's book one of the oddest and most beautiful books of the century. It was one of a very small number of British books displayed at the Great Exhibition of 1851 (no surprise, perhaps, since Whittingham was on one of the Juries of the exhibition). McLean goes on to say The result is a decided complication of Euclid, but a triumph for Charles Whittingham. Unfortunately, it is quite likely that the cost of publishing Byrne's book was a major cause of the firm's bankruptcy in 1853. More than 75% of the stock were still on hand.Whether or not Byrne's efforts complicate or simplify Euclid is an interesting and debatable point. Parts of Byrne's attempt to design `colour-coded' mathematical proofs are more successful than others, but it is our hope that even the less successful parts can serve as themes for discussion if not models for imitation. The title page of Byrne's edition, at any rate, illustrates the basic concept of the book rather nicely with a single figure illustrating Euclid's Proposition 47 (Pythagoras' Theorem).
The copy from which this image was taken is in the Colbeck collection of the Library of the University of British Columbia. It was purchased in auction in 1974 for about $300. Byrne's edition became well known recently when extracts from it were included and discussed in the second of Edward Tufte's books on graphical design. A copy of Byrne's book was auctioned in November, 1996 for US $3220.
About Oliver Byrne
We have not been able to find out much about Oliver Byrne, and would appreciate any information. From the little we have seen, we would hazard the opinion that in a country, a century, and a profession noted for eccentricity, Byrne was among the most eccentric. August De Morgan (in A Budget of Paradoxes) reviews the book The Creed of Athanasius by Mr. Byrne, in which he applies mathematical arguments to theology.- From the Creed: But the Godhead of the Father, of the Son, and of the Holy Ghost, is all One: the glory equal, the Majesty coeternal
- From Byrne: It has been shown that infinity, infinityf, infinityg, and (m infinity)s, together, are but infinity, and that each is infinity, and any magnitude in existence represented by infinity always was and always will be: for it cannot be made, or destroyed, and yet exists.
Byrne is also the author of a book Dual arithmetic also reviewed in A Budget of Paradoxes. The proposal is to replace the usual decimal notation ...
De Morgan's editor, the American historian of mathematics David Eugene Smith, doesn't like the idea of Byrne's edition of Euclid, either, but unfortunately we do not have De Morgan's opinion of it.
References
- Ruari McLean, Victorian book design & colour printing, Faber & Faber, 1963.
- A list of publications by Oliver Byrne

- Oliver Byrne's edition of 1847
- David Joyce's Java edition of Euclid
- Elizabeth Tuttle's wonderful guide to reading reading Euclid in Greek
- The Perseus project's Greek text of Euclid
- The Perseus project's collection of Heath's comments from his English edition of Euclid
- The integrated text (Byrne, Joyce, and Heath) at UBC
- A local collection of proofs of Pythagoras' Theorem in Java

- A Latin dictionary (Lewis & Short, at Perseus) to use while reading some of the material on this site
- A precursor - YBC 7289
- The Oxyrhynchus papyrus with the diagram for II.5
- The Clay Mathematics Institute history project , including images of the Bodleian Library's d'Orville MS (888 A.D.), the oldest extant copy of the Elements.
- Euclid in the Middle Ages, including a complete copy of a survey article and a list of extant manuscripts by Dr. Menso Folkerts.
- On Erhard Ratdolt, publisher of the 1482 edition of Euclid (the very first, based on the somewhat faulty medieval edition produced by Campanus)

- Images from Ratdolt's edition
- Images from the first English edition of 1582
- Selections from Sir Charles Thomas-Stanford's commentary on editions of Euclid
- Ralph Abraham's Visual elements
- The Euclid collection at University College, London
Writings of Oliver Byrne
- The Fifth Book of Euclid simplified, 1841.
- The Miscellaneous Mathematical Papers of OB, L. Maynard, ed. John Byrne, 1848.
- OB (ed) Appleton's Dictionary of machines, Mechanics, Engine work and Engineering, 2 vols, Daniel Appleton and Co., 1852.
- The Calculus of Form, 1870.
- The Creed of Saint Athanasius proved by a Mathematical parallel (a satire), 1859.
- Description and Use of the Byrnegraph, an instrument for multiplying, dividing and comparing lines, angles, surfaces and solids, Allard (London), 1846.
- Dual Arithmetic, A New Art, Bell & Daldy (London), 1865.
- The Essential Elements of Practical Mechanics, based on the principal of work, designed for engineering students, Spon (London), 1868.
- General Method of Solving Equations of all degress, applied particularly to equations of the second, third, fourth and fifth, Spon (London), 1868.
- The Geometry of Compasses, Lockwood (London), 1877.
- The Handbook for the Artisan, Mechanic, and Engineer, Collins (Philadelphia), 1853.
- How to Measure the Earth with the Assistance of Railroads, Currie and Bowman (Newcastle), 1838.
- Lectures on the Art and Science of War, Donahoe (Boston), 1853.
- New and Improved Systems of Logarithms, Day (London), 1838.
- Pocketbook for Railroad and Civil Engineers, Shepherd (New York), 1851.
- The Practical Metal-Worker's assistant, Baird (Philadelphia), 1851.
- The Practical Model Calculator, Baird (Philadelphia), 1852.
- A Short Practical Treatise on Spherical trigonometry, Valpy, 1835.
- Spon's Dictionary of Engineering, Spon, 1869 - 1874.
- Tables of Dual Logarithms, Dual Numbers, and corresponding Natural Numbers, Bell & Daldy, 1867
- Byrne's Treatise on navigation and nautical Astronomy, the author, 1875.
- The Young Dual Arithmetician, Bell & Daldy, 1865
- The Young Geometrician, or Practical geometry without compasses, Chapman and Hall (London), 1865.

No comments:
Post a Comment